Deborah O. Daniel, Sefiu A. Onitilo,
Omolade B. Benjamin, Ayoola A. Olasunkanmi
Olabisi Onabanjo University Ago Iwoye – Ogun State, Nigeria
https://doi.org/10.53656/nat2025-1.04
Abstract. Pneumonia and meningitis pose substantial threats to global public health due to their high morbidity and mortality rates. This study investigates the dynamics of these diseases with a focus on coinfection and evaluates the effectiveness of vaccination as a control measure. Using a mathematical model, the transmission dynamics are explored and the basic reproduction number is derived to identify conditions for disease-free and endemic states. Numerical simulations analyze the impact of varying vaccination compliance levels, demonstrating that higher compliance significantly reduces the number of susceptible and infected individuals while increasing the vaccinated population. The study emphasizes the need for integrated public health strategies combining vaccination campaigns, efficient vaccine distribution, and supportive medical care to mitigate the burden of pneumonia and meningitis coinfections. These findings provide a framework for designing effective interventions aimed at reducing disease prevalence and improving public health outcomes.
Keywords: Pneumonia; Meningitis; Coinfection; Mathematical Modelling; Transmission Dynamics, Vaccination; Sensitivity Analysis
-
Introduction
Infectious diseases remain a persistent challenge for public health systems worldwide, causing substantial illness and death. Among these, pneumonia and meningitis are particularly concerning due to their prevalence and severe consequences. Pneumonia, primarily caused by pathogens such as Streptococcus pneumoniae, is a major cause of death, particularly in young children and older adults (McLuckie 2009). Meningitis, commonly caused by bacteria like Neisseria meningitidis and Haemophilus influenzae, is a life-threatening condition that affects the brain and spinal cord, often resulting in significant fatalities or long-term disabilities (Fresnadillo Martínez et al. 2013; Afolabi et al. 2021). Addressing these diseases is a key priority for reducing their burden on global health.
Pneumonia affects the respiratory system and is transmitted through airborne particles. It is responsible for millions of deaths annually, with Streptococcus pneumoniae being a leading cause (World Health Organization, 1991). This bacterium is also linked to other serious infections, including meningitis and sinusitis (Opatowski et al. 2013; Kotola et al. 2022). Meningitis primarily targets the central nervous system and is associated with high mortality and long-term neurological complications (Zunt et al. 2018; Tilahun 2019). When pneumonia and meningitis occur together, they pose significant challenges to clinical management and public health efforts. This combination increases the severity of illness and places additional strain on healthcare systems (Tabatabaei et al. 2022; Chukwu et al. 2020). Despite these challenges, the mechanisms of coinfection remain insufficiently studied, leaving gaps in our understanding of effective treatment and prevention strategies.
Coinfection, where two or more pathogens infect a person simultaneously, has significant implications for disease progression, transmission, and treatment outcomes (Kehr & Engelmann, 2015). The combined occurrence of pneumonia and meningitis is particularly concerning, as it may worsen patient outcomes and complicate medical interventions (Obi et al. 2010; Kotola & Mekonnen 2022). Understanding the interplay between these infections is critical for developing effective public health strategies and improving clinical outcomes.
Mathematical modeling plays a pivotal role in understanding and addressing infectious diseases by offering frameworks to simulate disease dynamics and assess intervention strategies (Tilahun et al. 2018; Asamoah et al. 2018). According to Bailey (1975), the primary goal of mathematical modeling in epidemiology is to support informed decision-making. Models help evaluate the most cost-effective approaches to minimize the adverse impacts of diseases (Di Liddo 2016; Kizito & Tumwiine 2018). Researchers have developed models for pneumonia and meningitis individually, enhancing our understanding of their spread and informing control measures (Blyuss 2016; Joseph 2012; Musa et al. 2020). Pneumonia, for instance, has been the subject of extensive modeling efforts due to its significant global burden (McLuckie 2009; Joseph 2012). Tilahun (2019) utilized the SIR model to explore the co-dynamics of pneumonia and meningitis, contributing valuable insights into their interactions.
The application of mathematical models extends to evaluating vaccination and treatment strategies. For example, Tilahun et al. (2017) developed an SVCIR model to investigate cost-effective control strategies for pneumonia, concluding that a combination of prevention and treatment yields the most significant impact. Similarly, Onyinge et al. (2016) formulated models to analyze pneumonia coinfection with HIV/AIDS, highlighting the importance of combined intervention strategies. These efforts underscore the utility of mathematical frameworks in optimizing resource allocation for disease management.
In the case of meningitis, mathematical modeling has been instrumental in understanding its epidemiology and guiding control efforts. Meningitis remains a severe global health threat, particularly in resource-limited settings (Zunt et al. 2018; Ghia & Rambhad 2021; Abdullahi Baba et al. 2020). Outbreaks of bacterial meningitis, often caused by pathogens like Streptococcus pneumoniae and Neisseria meningitidis, demand urgent interventions (Van De Beek et al. 2010; Scarborough & Thwaites, 2008; Türkün et al. 2023). Models have been used to predict outbreak dynamics and assess the impact of vaccination programs (Jayaraman et al. 2018; Oordt-Speets et al. 2018; Kotola et al. 2022). For instance, the introduction of vaccines targeting Haemophilus influenzae type b and Streptococcus pneumoniae has significantly reduced the incidence of bacterial meningitis in high-income countries, though the burden persists in low- and middle-income regions (McIntyre et al. 2012; Peter et al. 2021).
Despite these advances, the combined dynamics of pneumonia and meningitis remain underexplored, particularly in the context of vaccination. Few studies have addressed their coinfection using mathematical models. Tilahun (2019) developed a model incorporating both diseases and emphasized the need for integrated approaches to improve intervention outcomes. Such efforts are essential for addressing the complexities of coinfection, where interactions between diseases may amplify severity and complicate treatment (Kotola & Mekonnen 2022; Chukwu et al. 2020). Still, studies on their combined dynamics remain limited, and existing models often fail to capture the combined effects of these diseases or explore the role of vaccination in reducing their impact. This highlights the need for a comprehensive approach to modeling pneumonia-meningitis coinfection, particularly in resource-constrained settings. This study seeks to address these gaps by constructing a mathematical model to examine the dynamics of pneumonia-meningitis coinfection considering the impact of vaccination.
-
Mathematical Formulation
In this study, we present a deterministic mathematical model designed to capture the transmission dynamics of pneumonia and meningitis coinfection within a population. The model divides the population into seven distinct compartments. These compartments include susceptible individuals (denoted as ), who are healthy but can be infected by pneumonia, meningitis, or both; vaccinated individuals (), who have received protection through vaccination; pneumonia-infected individuals (), who are infected solely with pneumonia and can transmit the disease to others; meningitis-infected individuals (), who are infected solely with meningitis; coinfected individuals (), who are infected by both pneumonia and meningitis; and recovered individuals (), representing those who have recovered from pneumonia, meningitis, or both diseases, or those who have removed themselves from the transmission cycle through vaccination.
The total population at any time is the sum of all these compartments, given by
![]()



The mathematical model proposed in this study aims to capture the transmission dynamics of pneumonia and meningitis coinfection, with a particular focus on the role of vaccination as a public health intervention. To keep the model tractable while still maintaining its ability to reflect real-world scenarios, several assumptions have been made which include the following:
- The population is homogeneous, with equal contact rates between individuals.
- Vaccination is modeled as a constant rate, affecting the overall population without individual-level variation.
- No cross-protection is assumed between pneumonia and meningitis.
- Vaccine effectiveness is constant across the entire population.
These assumptions balance the need for simplicity and computational feasibility with the necessity of accurately representing the underlying epidemiological processes.
2.1. Qualitative Analysis
2.1.1. Invariant Region


2.1.2. Positivity of the Solutions


2.2.1. The Effective Reproduction Number


2.2.2. Local Stability of the Disease-Free Equilibrium

2.2.3. Global Stability of the Disease-Free Equilibrium
Theorem 4. The disease-free equilibrium point is globally asymptotically stable

2.3. The Endemic Equilibria
The endemic equilibria represent the steady states where one or both infections persist in the population. We examine three cases: the pneumonia endemic equilibrium, the meningitis endemic equilibrium, and the coexistence equilibrium.
2.3.1. Pneumonia Endemic Equilibrium

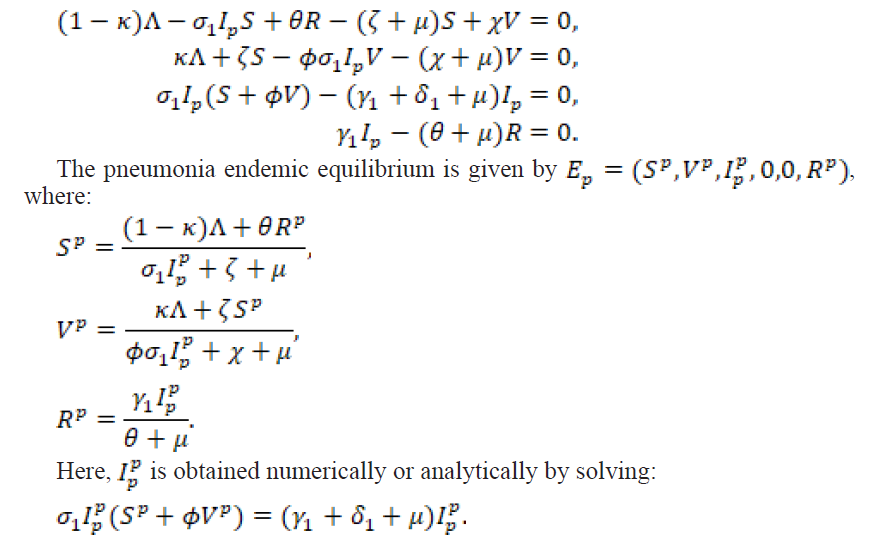
2.3.2. Meningitis Endemic Equilibrium


2.4. Sensitivity Analysis
In the study of epidemiology, it is critical to identify the factors that significantly contribute to disease transmission and prevalence. Sensitivity analysis serves as an essential method for assessing how variations in parameters influence the dynamics of a disease, enabling the development of targeted strategies to reduce both morbidity and mortality.
To evaluate the impact of parameters on the outcomes of the model, sensitivity indices are employed. These indices provide a measure of how a relative change in a parameter translates into a relative change in a state variable. The normalized forward sensitivity index is particularly useful in this context, as it quantifies the proportional effect of parameter variations on a given variable.

-
Numerical Simulations
This section presents the numerical simulation of the pneumonia-meningitis co-infection model, utilizing the baseline parameter values outlined in Table 1. Simulations were performed and visualized over time (in days) using MATLAB, with the resulting plots displayed in Figures 1 – 6.

Table 1. Parameters Description and Values Used in the Simulation Model
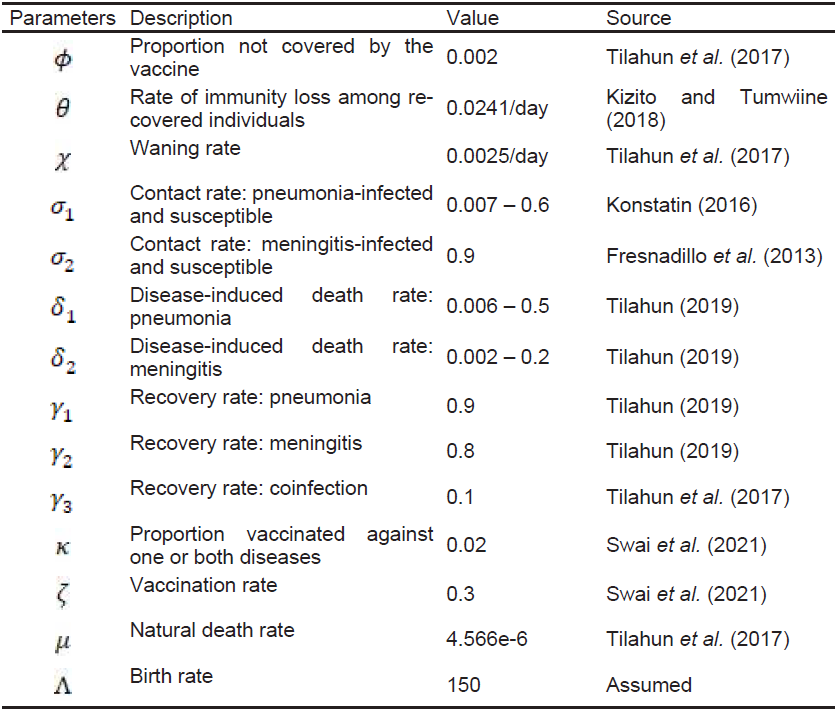
The numerical simulation of the effect of vaccination on the population dynamics is analysed using the baseline values given in Table 1. The numerical simulation are done and plotted against time (days) using MATLAB and the results are shown in Figures 1 – 6.
Figures 1 – 6 illustrates the impact of varying levels of vaccination effectiveness on the dynamics of a pneumonia-meningitis coinfection model over a period of 150 days. The figure compares scenarios with no vaccination, slightly effective vaccination (30% compliance), moderately effective vaccination (50% compliance), and highly effective vaccination (100% compliance). It demonstrates how these different levels of vaccination compliance affect the number of susceptible individuals (Figure 1), vaccinated individuals (Figure 2), pneumonia-infected individuals (Figure 3), meningitis-infected individuals (Figure 4), coinfected individuals (Figure 5), and recovered individuals (Figure 6).
As shown in Figure 1, the number of susceptible individuals decreases over time across all levels of vaccination effectiveness. Without any vaccination (denoted by dots), the decline in susceptible individuals is the least steep. The highly effective strategy (100% compliance) demonstrates the steepest decline. However, slightly effective (30% compliance) and moderately effective (50% compliance) strategies also show significant reductions, indicating a gradient effect of vaccination effectiveness on reducing the number of susceptible individuals.
Figure 2 displays the increase in vaccinated individuals over time. The graph shows that with higher compliance to vaccination (30%, 50%, and 100% effectiveness), the number of vaccinated individuals increases significantly compared to no vaccination. The highly effective strategy (100% compliance) results in the highest number of vaccinated individuals. Interestingly, the slightly effective strategy shows a quicker initial increase compared to the moderately effective strategy. This might be due to a higher initial vaccination uptake in the slightly effective scenario, which could be attributed to increased public awareness or access to vaccines.
As displayed in Figure 3, the number of pneumonia-infected individuals decreases over time. The graph shows that with no vaccination (denoted by dots), the reduction is the slowest. Slightly effective (30% compliance) and moderately effective (50% compliance) vaccination strategies result in a more significant decrease, but the highly effective strategy (100% compliance) shows the most substantial reduction in pneumonia infections. The slightly effective strategy appears to reduce infections quicker than the moderately effective one. This could be due to initial variations in how the vaccine impacts different population subsets or logistical differences in vaccine distribution and uptake.
Figure 4 shows the trends for meningitis-infected individuals. Similar to pneumonia, the graph demonstrates a decrease in meningitis infections over time. The reduction is least significant without vaccination. The slightly effective strategy initially performs better than the moderately effective one, which might be due to similar reasons as discussed for pneumonia: initial vaccine impact variations and differences in vaccine distribution logistics. The highly effective strategy (100% compliance) leads to the most considerable decline in meningitis infections.
In Figure 5, the number of coinfected individuals (infected with both pneumonia and meningitis) increases over time across all strategies. The rate of increase is highest without any vaccination (denoted by dots) and progressively decreases with more effective vaccination strategies. The highly effective strategy (100% compliance) shows the slowest increase. Interestingly, the slightly effective strategy shows a lower rate of increase compared to the moderately effective strategy at certain points, potentially due to initial population dynamics and vaccine distribution efficiency.
Figure 6 depicts the number of recovered individuals over time. The number of recoveries is lowest with no vaccination and increases with the effectiveness of the vaccination strategy. However, the difference in the number of recoveries among the slightly effective, moderately effective, and highly effective strategies is minimal. This small difference indicates that while vaccination does contribute to recovery, its impact on this specific outcome is less pronounced compared to its effect on reducing the number of susceptible and infected individuals.
The slightly effective strategy shows better initial performance in some graphs due to variations in how different population subsets respond to the vaccine. Some individuals might have a quicker immune response, leading to an initial rapid decline in infections or an increase in recoveries. Differences in how the vaccine is distributed and administered can impact initial results. Efficient distribution in the slightly effective scenario might lead to quicker initial results compared to a more evenly distributed but slower uptake in the moderately effective scenario. Higher public awareness or better access to vaccines in the slightly effective scenario might result in a quicker initial response, leading to better performance in the early stages. The small difference in the number of recovered individuals among the different vaccination strategies suggests that other factors, such as natural recovery rates and the effectiveness of medical treatments, play a significant role in recovery. To enhance the impact of vaccination on recovery rates, it might be necessary to combine vaccination with improved medical treatments and supportive care. Improving the logistics of vaccine distribution to ensure a more uniform and efficient rollout can help achieve better initial results across all effectiveness levels. By addressing any logistical challenges, we can ensure that vaccines reach the population more quickly and evenly. Implementing campaigns to raise awareness about the importance of vaccination can increase uptake and compliance, improving overall effectiveness. These campaigns can educate the public on the benefits of vaccination and encourage more people to get vaccinated.
Regularly monitoring how different population subsets respond to the vaccine can help adjust strategies to maximize effectiveness. This monitoring can identify which groups are responding well and which may need additional support or different strategies.
To enhance the impact of vaccination on recovery rates, it is important to also focus on improving medical treatments and supportive care for infected individuals. Combining vaccination with better medical care can ensure that those who contract the disease receive the best possible treatment, further reducing the overall impact of the infection.
Despite some initial better performance in the slightly effective strategy, the highly effective vaccination strategy (100% compliance) remains the best approach in the long run. It results in the steepest decline in susceptible and infected individuals and the highest number of vaccinated individuals. While the impact on recovered individuals is less pronounced, achieving high compliance with vaccination significantly improves public health outcomes by reducing infection rates and increasing recovery in combination with effective medical care.
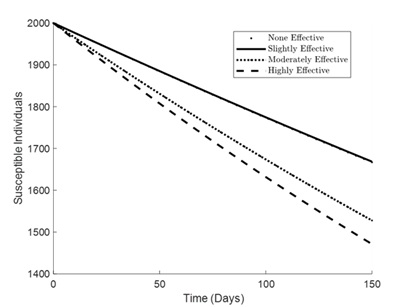
Figure 1. Simulation effect of vaccination on the susceptible individuals
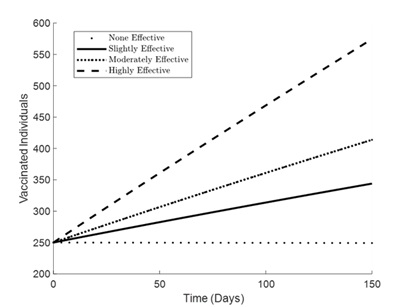
Figure 2. Simulation effect of vaccination on the vaccinated individuals
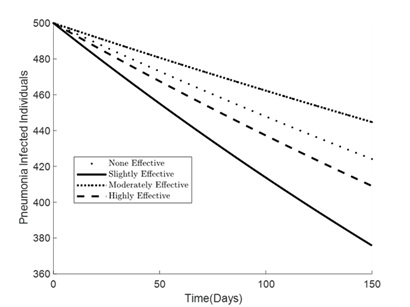
Figure 3. Simulation effect of vaccination on the pneumonia-infected individuals
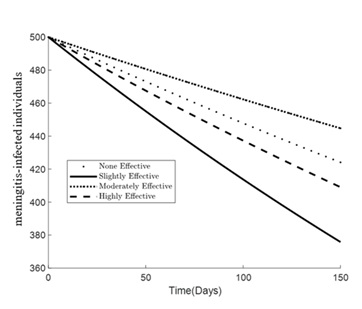
Figure 4. Simulation effect of vaccination on the meningitis-infected individuals
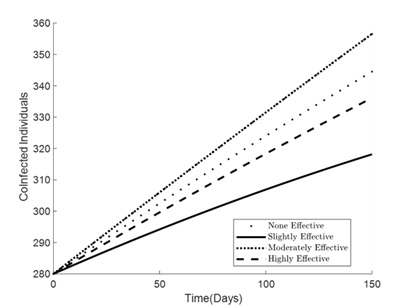
Figure 5. Simulation effect of vaccination on the co-infected individuals
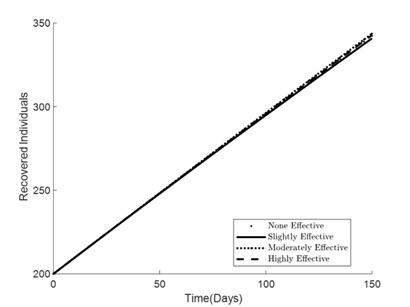
Figure 6. Simulation effect of vaccination on the recovered individuals
3.1. Sensitivity Index


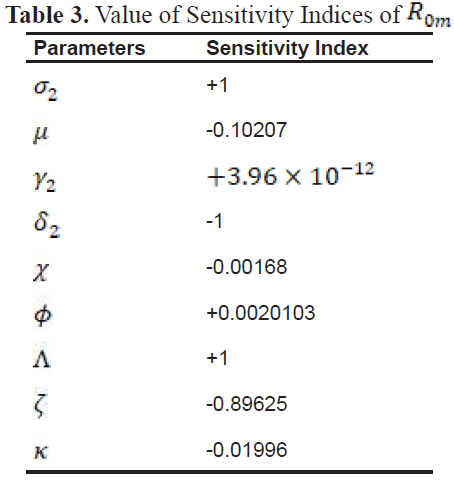
-
Conclusion
This study presents a compartmental deterministic mathematical model of the dynamics of pneumonia and meningitis coinfection. It highlights the important role of vaccination in controlling the spread of both diseases within a population. Our analysis demonstrates that varying levels of vaccination compliance can notably reduce the number of susceptible and infected individuals, with higher vaccination compliance leading to the most considerable reductions. Although the effect of vaccination on recovery rates is less pronounced, the combination of high vaccination coverage and improved medical care offers significant public health benefits.
The findings emphasize the need to address logistical challenges, increase public awareness, and improve vaccine accessibility to maximize the effectiveness of vaccination programs. While slightly effective strategies may show initial success, the long-term impact is most pronounced with highly effective vaccination coverage. Therefore, to optimize public health outcomes, it is crucial to expand vaccination campaigns, enhance distribution logistics, and integrate vaccination with improved medical treatments. Regular monitoring and adjustments to vaccination strategies, based on population responses, will further enhance the effectiveness of disease control measures.
While the model does not explicitly capture variations in immune responses or the logistics of vaccine distribution, it simplifies the vaccine impact by assuming that vaccination reduces susceptibility in proportion to the coverage level. The vaccine’s effectiveness is modeled as a constant factor in the transition dynamics between compartments, reflecting an overall reduction in susceptibility and infection. Further refinements to the model could include the influence of varying immune responses or more detailed vaccine administration strategies, but these aspects were not included in the current study.
REFERENCES
AFOLABI, M. A., ADEWOYE, K. S., FOLORUNSO, A. I., ET AL., 2021. A mathematical model on transmission dynamics of meningococcal meningitis. Iconic Research and Engineering Journals, vol. 4, no. 10, pp. 59 – 66.
ASAMOAH, J.K.K., NYABADZA, F., SEIDU, B. et al., 2018. Mathematical modelling of bacterial meningitis transmission dynamics with control measures. Computational and Mathematical Methods in Medicine. https://doi.org/10.1155/2018/2657461.
BAILEY, N. T. J., 1975. The Mathematical Theory of Infectious Diseases and Its Applications (2nd ed.). Charles Griffin & Company Ltd.
BLYUSS, K. B., 2016. Mathematical modelling of the dynamics of meningococcal meningitis in Africa. In: P. Aston, A. Mulholland, K. Tant (Eds.). UK Success Stories in Industrial Mathematics, pp. 221 – 226. Springer, Cham.
CHUKWU, C. W., MUSHANYU, J., JUGA, M. L., ET AL., 2020. A mathematical model for co-dynamics of listeriosis and bacterial meningitis diseases. Communications in Mathematical Biology and Neuroscience, pp. 1 – 25.
DI LIDDO, A., 2016. Optimal control and treatment of infectious diseases: The case of huge treatment costs. Mathematics, vol. 4, no. 2, p. 21.
FRESNADILLO MARTÍNEZ, M.J., GARCÍA MERINO, E., GARCÍA SÁNCHEZ, E. ET AL., 2013. A mathematical model to study the meningococcal meningitis. Procedia Computer Science, vol. 18, pp. 2492 – 2495.
GHIA, C. J., & RAMBHAD, G. S., 2021. A systematic literature review on the prevalence and etiology of meningitis among critically ill and hospitalized patients in India. Therapeutic Advances in Infectious Disease, vol. 8. https://doi.org/10.1177/20499361211046453.
JAYARAMAN, Y., VEERARAGHAVAN, B., CHETHRAPILLY PURUSHOTHAMAN, G. K., ET AL., 2018. Burden of bacterial meningitis in India: Preliminary data from a hospital-based sentinel surveillance network. PLoS One, vol. 13, no. 5, p. e0197198.
JOSEPH, E., 2012. Mathematical Analysis of Prevention and Control Strategies of Pneumonia in Adults and Children. (Doctoral dissertation). University of Dar es Salaam.
KIZITO, D., & TUMWIINE, J., 2018. A mathematical model of treatment and vaccination interventions of pneumococcal pneumonia. Journal of Applied Mathematics. https://doi.org/10.1155/2018/2539465.
KOTOLA, B. S., & MEKONNEN, T. T., 2022. Mathematical model analysis and numerical simulation for codynamics of meningitis and pneumonia infection with intervention. Scientific Reports, vol. 12, pp. 1 – 18.
KOTOLA, B. S., GEBRU, D. M., & ALEMNEH H. T., 2022. Appraisal and simulation on codynamics of pneumonia and meningitis with vaccination intervention. Computational and Mathematical Methods in Medicine, pp. 1 – 20.
KEHR, J., & ENGELMANN, L., 2015. Double trouble: Towards an epistemology of co-infection. Medicine, Anthropology, Theory, vol. 2, no. 1, pp. 1 – 31.
MCINTYRE, P. B., O’BRIEN, K. L., GREENWOOD, B., & VAN DE BEEK, D., 2012. Effect of vaccines on bacterial meningitis worldwide. The Lancet, vol. 380, no. 9854, pp. 1703 – 1711.
MCLUCKIE, A., 2009. Respiratory Disease and Its Management. Springer Science & Business Media.
MUSA, S. S., ZHAO, S., H., NAFIU, H., ET AL., 2020. Mathematical modeling and analysis of meningococcal meningitis transmission dynamics. International Journal of Biomathematics, vol. 13, no. 1, p. 2050006.
ONYINGE, D., ONGATI, N., & ODUNDO, F., 2016. Mathematical model for co-infection of pneumonia and HIV/AIDS with treatment. International Journal of Science, Engineering and Applied Sciences, vol. 2, no. 1, pp. 106 – 111.
OORDT-SPEETS, A. M., BOLIJN, R., VAN HOORN, R. C., ET AL., 2018. Global etiology of bacterial meningitis: A systematic review and meta-analysis. PLoS One, vol. 13, no. 6, p. e0198772.
OPATOWSKI, L., VARON, E., DUPONT, C., ET AL., 2013. Assessing pneumococcal meningitis association with viral respiratory infections and antibiotics: insights from statistical and mathematical models. Proceedings of the Royal Society B, vol. 280, p. 20130519.
PETER, O.J., YUSUF, A., OSHINUBI, K. ET AL., 2021. Fractional order of pneumococcal pneumonia infection model with Caputo Fabrizio operator. Results in Physics, vol. 29, p. 104581.
SCARBOROUGH, M., & THWAITES, G. E., 2008. The diagnosis and management of acute bacterial meningitis in resource-poor settings. The Lancet Neurology, vol. 7, no. 7, pp. 637 – 648.
TABATABAEI, S. R., SHAMSHIRI, A., AZIMI, L., ET AL., 2022. Co-infection with dual Streptococcus pneumoniae serotypes as a cause of pediatric bacterial meningitis in Iran: A multi-center cross-sectional study. BMC Infectious Diseases, vol. 22, no. 1, p. 625.
TILAHUN, G. T., 2019. Modeling co-dynamics of pneumonia and meningitis diseases. Advances in Difference Equations, pp. 1 – 18.
TILAHUN, G. T., MAKINDE, O. D., & MALONZA, D., 2017. Modeling and optimal control of pneumonia disease with cost-effective strategies. Journal of Biological Dynamics, vol. 11, no. 2, pp. 400 – 426.
TÜRKÜN, C., GÖLGELI, M. & ATAY, F.M., 2023. A mathematical interpretation for outbreaks of bacterial meningitis under time-dependent transmission parameters. Nonlinear Dynamics, vol. 111, p. 14467 – 14484.
VAN DE BEEK, D., FARRAR, J. J., GANS, J., ET AL., 2010. Adjunctive dexamethasone in bacterial meningitis: A meta-analysis of individual patient data. The Lancet Neurology, vol. 9, no. 3, pp. 254 – 263.
WORLD HEALTH ORGANIZATION, 1991. Technical Bases for the WHO Recommendations on the Management of Pneumonia in Children at First-Level Health Facilities. World Health Organization.
ZUNT, J. R., KASSEBAUM, N. J., BLAKE, N., ET AL., 2018. Global, regional, and national burden of meningitis, 1990–2016: A systematic analysis for the global burden of disease study 2016. The Lancet Neurology, vol. 17, no. 12, pp. 1061 – 1082
Dr. Deborah O. Daniel
ORCID iD: 0000-0003-4025-1448
Olabisi Onabanjo University
Ago-Iwoye, Ogun State, Nigeria
E-mail: oludeboradaniel@gmail.com
Sefiu A. Onitilo
ORCID iD: 0000-0002-4418-197X
Olabisi Onabanjo University
Ago Iwoye, Ogun State, Nigeria
E-mail: onitilo.sefiu@oouagoiwoye.edu.ng
Omolade B. Benjamin
ORCID iD: 0009-0004-0665-5558
Olabisi Onabanjo University
Ago Iwoye, Ogun State, Nigeria
E-mail: omoladebabajide342@gmali.com
Ayoola A. Olasunkanmi
ORCID iD: 0009-0006-3530-5391
Olabisi Onabanjo University
Ago Iwoye, Ogun State, Nigeria
E-mail: ayoolaolasunkanmi243@mail.com
> Download the article as a PDF file <<



